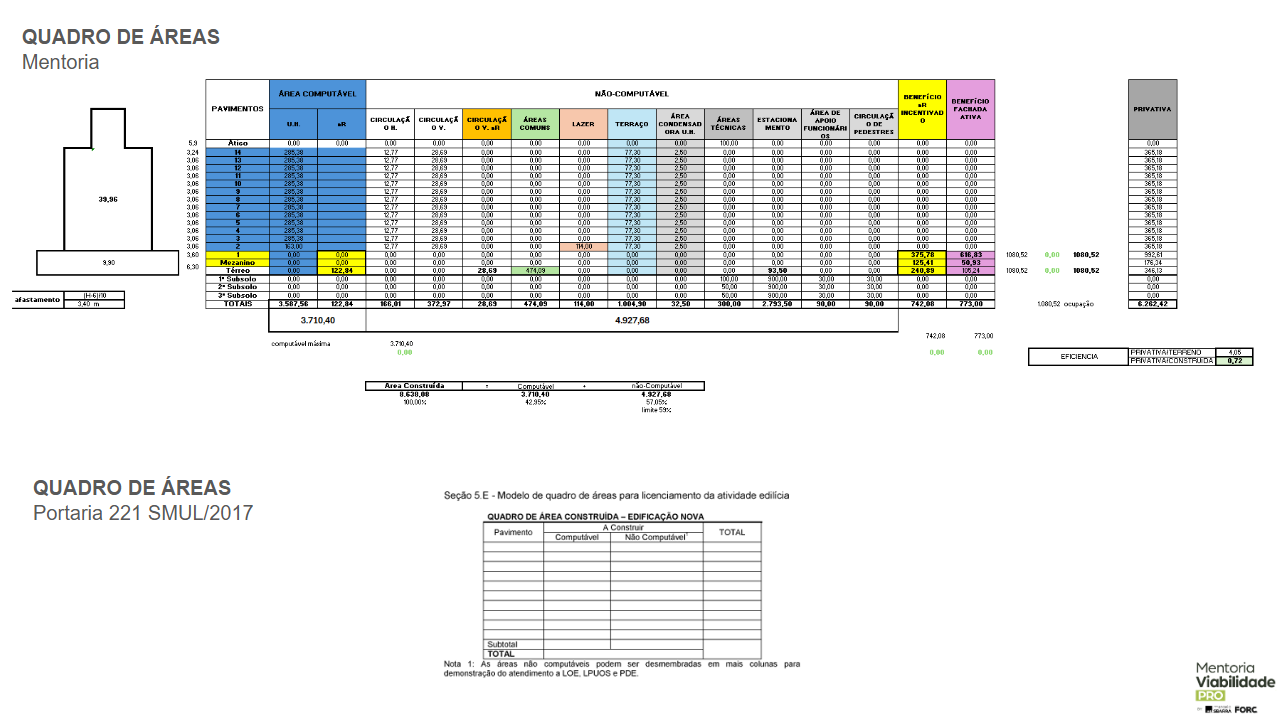
Neste artigo vou mostrar como desenhar um Eneágono – que servirá de base para a construção do nosso Octodecágono (Polígono regular de 18 lados).
Por ser um Polígono regular, o Eneágono possui as seguintes características:
- todos os seus lados são iguais
- todos os seus ângulos (internos e externos) são iguais;
O Eneágono possui, desta forma, 9 lados iguais, 9 vértices (um vértice corresponde ao ponto de interseção de dois lados de uma figura geométrica) e 9 ângulos internos iguais a 140º.
Por ser um Polígono Regular, o Eneágono pode ser inscrito em uma circunferência: isto nos permite construir a figura acima através de traçados geométricos.

O vídeo abaixo* mostra o passo a passo da construção do Eneágono:
- Trace um segmento de reta qualquer AZ;
- marque um ponto Y neste segmento (mais para próximo de Z);
- Trace a Mediatriz do segmento de reta AY, encontrando o Ponto Médio X;
- Com a ponta seca do compasso em X, race a circunferência de raio AX: dentro desta circunferência que estará inscrito o nosso Eneágono!
- Marque os pontos U e V, onde a nossa circunferência cortou a Mediatriz;
- Com a ponta seca em U e raio UX, trace uma circunferência auxiliar: ela cortará a nossa circunferência principal no ponto T;
- Com a ponta seca do compasso em V e raio VT, trace uma segunda circunferência auxiliar: ela cortará o segmento de reta AZ no ponto S;
- Com a ponta seca em S e raio SU, trace uma nova circunferência auxiliar:la cortara o segmento de reta AZ no ponto R;
- Com a ponta seca em A e raio AR trace nova circunferência auxiliar: ela cortará a nossa circunferência principal no ponto I: a distância AI é o lado do nosso Eneágono!
- A partir do vértice A, pegue a distância AI e marque ao redor da circunferência, encontrando os demais vértices;
- Pronto! O Eneágono está desenhado!
[cite]
Observação importante: estas informações são direcionadas a projetos acadêmicos – para projetos “da vida real” é indispensável a contratação de um Arquiteto para a verificação das necessidades de seu projeto e adequações à legislação de sua municipalidade.
© Marcelo Sbarra. Os projetos mostrados neste artigo são protegidos pela Lei de Direito Autoral (Lei 9.610/98) e Resolução 67/2013 do CAU/BR.